- Mechanik Newtons
- Newtons Gesetze
- Zusammensetzung von zwei wirkenden Kräften
- Wirken in eine Richtung
- Wirken in entgegengesetzte Richtungen
- Anderweitiges Wirken
- Newton I – Das Trägheitsgesetz
- Newton II – Das newtonsche Grundgesetz
- Newton III – Das Wechselwirkungsgesetz
- Eindimensionale Bewegungen
- Bewegungsdiagramme
- Gleichförmige geradlinige Bewegung (a = 0)
- Gleichmäßig beschleunigte geradlinige Bewegung (F = konst. ≠ 0)
- Beschleunigte geradlinige Bewegung (a ≠ konst.)
- Harmonische Schwingungen
- Fadenpendel
- Federpendel
- Energie als Erhaltungsgröße
- Impuls als Erhaltungsgröße
- Zweidimensionale Bewegungen
- Waagerechter Wurf
- Gleichförmige Kreisbewegung
- Zentripetalkraft
- Gravitationsgesetz
- Grenzen der Gültigkeit der newtonschen Mechanik
- Kausalitätsprinzip
- Spezielle Relativitätstheorie
- Längenkontraktion und Zeitdilation
- Addition von Geschwindigkeiten
- Relativität der Masse
- Äquivalenz von Masse und Energie
Mechanik Newtons
Newtons Gesetze
Zusammensetzung von zwei wirkenden Kräften
Hat man zwei Kräfte, die auf einen Körper wirken, stellt man sich die Frage, wie dieser bewegt wird. Hierfür ist maßgeblich, wie sich die Kräfte zueinander verhalten.
Wirken in eine Richtung
Wirken die untersuchten Kräfte in eine Richtung, so kann man die Beträge addieren. Die Kräfte werden durch Pfeile dargestellt, deren Länge der jeweiligen Stärke entspricht. Man erhält durch das Aneinanderlegen dieser die Gesamtkraft.
Wirken in entgegengesetzte Richtungen
Wirken die Kräfte entgegengesetzt, zeigen die Pfeile also in die umgekehrte Richtung, so subtrahiert man sie.
Anderweitiges Wirken
Wirken die Kräfte anderweitig zueinander (sie wirken also nicht parallel), so erhält man die Gesamtkraft mithilfe eines Kräfteparallelogramms, in dem die beiden Kräfte je zwei Seiten darstellen.
Newton I – Das Trägheitsgesetz
Das erste newtonsche Gesetz setzt sich mit der Trägheit von Körpern auseinander. Demnach setzt ein Körper seinen momentanen Zustand fort, wenn auf ihn keine Kraft wirkt oder die auf die ihn einwirkenden Kräfte in der Summe 0 ergeben.
Newton II – Das newtonsche Grundgesetz
Nach dem newtonschen Grundgesetz gilt Folgendes: Wirkt auf einen Körper der Masse m eine Kraft F, so erfährt er die Beschleunigung a.
Für die gleichmäßige Beschleunigung eines Körpers aus dem Stillstand gelten, wenn die Beschleunigung a konstant ist, folgende Zusammenhänge:
Newton III – Das Wechselwirkungsgesetz
Nach dem Wechselwirkungsgesetz gilt: Wirken zwei Körper aufeinander, so wirkt auf beide Körper eine gleich große entgegengesetzt gerichtete Kraft:
Eindimensionale Bewegungen
Bewegungsdiagramme
Gleichförmige geradlinige Bewegung (a = 0)
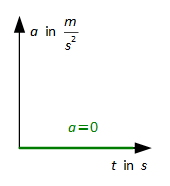
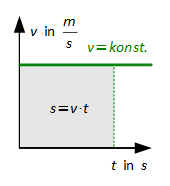
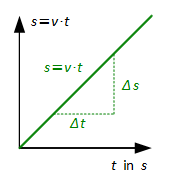
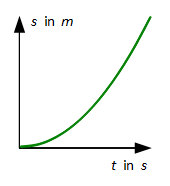
Gleichmäßig beschleunigte geradlinige Bewegung (F = konst. ≠ 0)
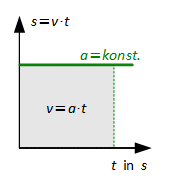
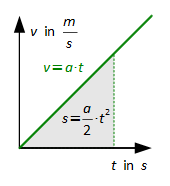
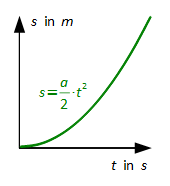
Beschleunigte geradlinige Bewegung (a ≠ konst.)
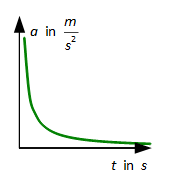
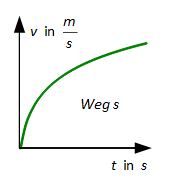
Harmonische Schwingungen
Eine mechanische Schwingung ist eine zeitlich periodische Bewegung eines Körpers um eine Gleichgewichtslage. Zum Erzeugen müssen folgende Dinge vorhanden sein:
- Schwingungsfähiger Körper
- Körper ausgelenkt aus seiner Gleichgewichtslage (Kraft bzw. Energie benötigt)
- Kraft, die den Körper zu Gleichgewichtslage zurücktreibt
Ein Beispiel ist etwa, wenn eine Masse m an ein Federpendel gehängt und aus der Gleichgewichtslage gelenkt wird.
Es wirkt eine Federkraft F:
Daraus ergibt sich wiederum folgende Gleichung:
Eine Schwingung, bei der die zurücktreibende Kraft F ∼ Auslenkung y ist, nennt man harmonische Schwingung. Als Auslenkung y bezeichnet man den Abstand zur Gleichgewichtslage, der Elongation. Hat man ein t-y-Diagramm mit einer harmonischen Schwingung, so ist deren Graph eine Sinuskurve. Jene werden deshalb auch Sinusschwingung genannt.
Die Amplitude A (Einheit: 1 m) ist der größte Abstand des schwingenden Körpers zur Ruhelage. Die Schwingungs- bzw. Periodendauer ([T] = 1 s) gibt die Zeit für eine Schwingung an. Die Frequenz f einer Schwingung gibt an, wie viele Schwingungen pro Sekunde ablaufen.
- Formelzeichen: f
- Einheit: 1 Hertz bzw. $\mathrm{1\,Hz = 1 \cdot s^{-1}}$
Die Frequenz kann berechnet werden mit:
Dabei ist T die Schwingungsdauer, n die Anzahl der Schwingungen und t die benötigte Zeit für n Schwingungen.
Für die harmonische Schwingung lautet die Funktionsgleichung y(t):
A ist hier die Amplitude, t die Zeit, T die Schwingungsdauer und ω die Kreisfrequenz.
Fadenpendel
Für die Schwingungsdauer eines Fadenpendels gilt unter Bedingung der kleinen Auslenkung aus der Ruhelage:
Dabei ist l die Länge des Fadenpendels.
Federpendel
Für die Schwingungsdauer eines Federpendels gilt:
Dabei ist m die Masse des schwingenden Körpers und D die Federkonstante
Energie als Erhaltungsgröße
Mit Energie kann ein Körper verformt, erwärmt oder zur Strahlenaussendung gebracht werden. In einem abgeschlossenen System bleibt die Gesamtenergie E erhalten, es gilt:
Impuls als Erhaltungsgröße
Der Impuls p ist das Produkt aus der Masse m und der Geschwindigkeit v:
In einem abgeschlossenen System bleibt der Gesamtimpuls P erhalten:
Zweidimensionale Bewegungen
Waagerechter Wurf
Ein waagerechter Wurf setzt sich aus einer gleichförmigen Bewegung in x-Richtung und einer in vertikaler Richtung gleichförmigen Bewegung zusammen, die unabhängig voneinander sind. Dabei gilt für den Aufenthaltsort eines Körpers nach einer bestimmten Zeit t:
Die Bahnkurve ist Teil einer Parabel:
Die Wurfdauer t ist nur von der Höhe h abhängig:
Die Wurfweite ist abhängig von der Anfangsgeschwindigkeit v0 und von der Höhe h:
Gleichförmige Kreisbewegung
Zu unterscheiden sind Kreis- und Drehbewegungen. Eine Kreisbewegung ist vorhanden, wenn der Körper als Massepunkt angesehen werden kann, z.b. bei einer Gondel eines Riesenrads. Die Drehbewegung ist z. B. die Bewegung des Riesenrads an sich. Ein Vergleich beider zeigt:
- Der Betrag der Geschwindigkeit ist konstant
- Bei der gleichförmigen Kreisbewegung ändert sich die Richtung der Geschwindigkeit; es liegt eine beschleunigte Bewegung vor
Die Geschwindigkeit v ist dabei abhängig vom Radius der Kreisbahn r und der Umlaufzeit T:
Die Winkelgeschwindigkeit ω gibt an, wie schnell sich der Drehwinkel φ (oder φ in Bogenmaß) ändert. Die Einheit ist deshalb der Quotient aus der Änderung des Winkels in einer bestimmten Zeit:
Bei einer gleichförmigen Kreisbewegung gilt für die Geschwindigkeit v:
Daraus ergibt sich, dass – unter der Bedingung, dass die Winkelgeschwindigkeit ω konstant ist – die Geschwindigkeit v größer wird, wenn der Radius r größer wird und dass bei konstantem Radius die Geschwindigkeit größer wird, je größer die Winkelgeschwindigkeit ist.
Zentripetalkraft
Die Zentripetalkraft FZ wird benötigt, um einen Körper auf einer gleichförmigen Kreisbahn zu bewegen. Die Kraft ist auf den Mittelpunkt des Kreises gerichtet. Für die Zentripetalkraft einer gleichförmigen Kreisbewegung gilt:
Bewegt sich der Körper auf der Kreisbahn, so wirkt eine gleich große entgegengesetzte Kraft, die Zentrifugalkraft.
Gravitationsgesetz
Zwischen einem Körper der Masse m und einem zweiten Körper der Masse M wirken Anziehungs- bzw. Gravitationskräfte. Die wirkende Gravitationskraft FG ist neben den Massen auch vom Abstand r der Massenmittelpunkte abhängig:
Dabei ist G die Gravitationskonstante:
Grenzen der Gültigkeit der newtonschen Mechanik
Kausalitätsprinzip
Für viele Bereiche der Physik, Technik und des Alltags gilt das Prinzip der starken Kausalität: Ähnliche Ursachen haben ähnliche Wirkungen.
Es gibt aber auch Situationen, in denen die Anfangsbedingungen leicht verändert werden können und die Wirkungen sehr variieren. Die starke Kausalität ist verletzt, obwohl die Aussage der gleichen Wirkung bei gleicher Ursache gelten kann. Man nennt dies das Prinzip der schwachen Kausalität.
Liegt eine starke Kausalität in einem System vor, dann auch eine schwache. Das Verhalten könnte man bei exakter Kenntnis der Bedingungen vorhersagen, was in der Praxis jedoch nicht möglich ist. Man spricht hier vom deterministischen Chaos. Die Verletzung der starken Kausalität führt zu Vorgängen, die auf lange Zeit hin betrachtet nicht vorhersagbar sind.
Spezielle Relativitätstheorie
Albert Einstein (1879-1955) begründete die spezielle Relativitätstheorie, die auf den Prinzipien der Relativität und der Konstanz der Lichtgeschwindigkeit beruht.
Das Relativitätsprinzip besagt, dass sich in mit konstanter Geschwindigkeit zueinander bewegenden Bezugssystemen die physikalischen Gesetze gleich wirken. Das zweite Prinzip besagt, dass sich Licht im Vakuum immer mit der Lichtgeschwindigkeit c ausbreitet:
Längenkontraktion und Zeitdilation
Betrachtet man Körper und Uhren, die sich relativ zu einem Beobachter schnell bewegen, scheinen die Körper sich für diesen in Bewegungsrichtung zu verkürzen bzw. gehen die Uhren langsamer. Wie groß die Effekte ausfallen, kann man mit dem Lorentzfaktor γ herausfinden:
Aufgrund dieser Formel ist es auch nicht möglich, die Lichtgeschwindigkeit zu erreichen oder zu übersteigen. Wäre die Geschwindigkeit v so groß wie die Lichtgeschwindigkeit, hätte man im Nenner des Bruchs 0, was nicht berechenbar ist.
Um die Längenkontraktion zu erhalten, muss man den Faktor γ mit der Länge des Körpers in Verbindung setzen:
Bei der Zeitdilatation gilt:
Addition von Geschwindigkeiten
Für Geschwindigkeiten unter zehn Prozent der Lichtgeschwindigkeit gilt, dass die Summe der Geschwindigkeiten v1 und v2 die Geschwindigkeit v ergibt:
Über dieser „Grenze“ ist dies nicht der Fall, da relativistische Effekte eine Rolle spielen. Die Geschwindigkeiten addieren sich so, dass die Summe immer kleiner oder gleich der Lichtgeschwindigkeit ist.
Relativität der Masse
Je näher die Geschwindigkeit v eines Körpers oder Teilchens der Lichtgeschwindigkeit c kommt, desto mehr nimmt seine Masse zu:
Äquivalenz von Masse und Energie
Die Gesamtenergie E eines Körpers ist proportional zu seiner Masse m. Es gilt:
Da c eine Konstante ist, sind Energie und Masse das Gleiche mit unterschiedlichen Einheiten. Dabei entspricht eine Energie von 1 J einer Masse von circa 10-14 g.