- Funktionale Zusammenhänge
- Direkte Proportionalität
- Indirekte Proportionalität
- Funktionen
- Der Funktionsbegriff
- Beispiel
- Lineare Funktionen
- Funktionen der direkten Proportionalität
- Die lineare Funktion
- Eigenschaften
- Ungleichungen
- Lineare Gleichungssysteme: Rechnerisches Lösen
- Das Gleichsetzungsverfahren
- Beispiel
- Das Einsetzverfahren
- Beispiel
- Das Additionsverfahren
- Beispiel
- Laplace-Experimente
- Das Zufallsexperiment
- Das Ereignis
- Das Zählprinzip
- Gebrochenrationale Funktionen
- Beispiele für gebrochenrationale Funktionen
- Strahlensätze und Ähnlichkeit
- Ähnlichkeit
- Der Vierstreckensatz oder Strahlensatz
Funktionale Zusammenhänge
Direkte Proportionalität
Es werden in zwei Behälter - einer mit der Form eines Zylinders und der andere die eines Kegels - jeweils 0,4 Liter Wasser geschüttet und die entsprechende Füllhöhe gemessen. Dabei könnte man als Messergebnisse folgendes erhalten:
| V in l | 0 | 0,1 | 0,2 | 0,3 | 0,4 |
| Höhe 1 in cm | 0 | 1,9 | 3,9 | 6,9 | 15 |
| Höhe 2 in cm | 0 | 2,1 | 4,2 | 6,3 | 8,4 |
Für das Volumen V und die Füllhöhe h ergibt sich der Zusammenhang:
Dieser Quotient hat stets den gleichen Wert (ausgenommen für h = 0). Dieser Wert wird als Proportionalitätsfaktor bezeichnet.
Allgemein lässt sich sagen, dass zwei Größen x und y zueinander proportional heißen, wenn der Faktor a beiden Größen zugeordnet werden kann. Deren Quotient hat dabei stets den gleichen Wert.
In einem Liniendiagramm ist der Graph eine Ursprungsgerade. Wenn von einem Paar ein Wert gegeben, so kann man weitere Werte berechnen.
Indirekte Proportionalität
Beispiel: Für ein Sportfest sollen 2400 Flyer verteilt werden. Wie viele Flyer muss ein Schüler verteilen, wenn x Personen Flyer verteilen?
| x | 10 | 20 | 30 | 40 | 50 |
| Flyer | 240 | 120 | 80 | 60 | 48 |
| Produkt | 2400 | 2400 | 2400 | 2400 | 2400 |
Bei der indirekten Proportionalität ist das Produkt zweier Werte stets gleich. Zeichnet man den Graphen in ein Diagramm, so erhält man eine Hyperbel.
Funktionen
Der Funktionsbegriff
Eine eindeutige Zuordnung zweier Größen nennt man Funktion f. Kann man diese Funktion durch einen Term darstellen, so nennt man diesen Funktionsterm f(x).
Werte von x, für die der Funktionswert 0 ist, heißen Nullstellen. Diese kann man berechnen, indem man die Gleichung mit 0 gleichsetzt und dann nach x auflöst.
Beispiel
Die Faustregel für den Reaktionsweg lautet: „Geschwindigkeit in km/h geteilt durch 10 mal 3 = Reaktionsweg in m“. Nimmt man für die Geschwindigkeit den Wert x, erhält man folgenden Term:
Durch Gleichsetzen erhält mit Null erhält man als Nullstelle den Wert x = 0.
Lineare Funktionen
Funktionen der direkten Proportionalität
Man kauft einen Gegenstand zu einem Preis von 1,5. Kauft man nun zwei Stück davon, kosten diese 3, bei drei 4,5 etc. Der Proportionalitätsfaktor 1,5 bzw. die Zuordnung kann man durch die Funktionsgleichung f(x)= mx = 1,5x beschreiben.
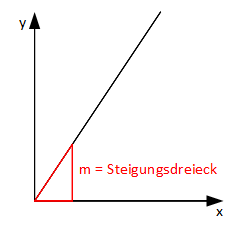
Allgemein beschreibt die Funktion f mit der Gleichung
![]() eine direkte Propotionalität von x und y. Dabei
gibt m die Steigung des Graphs an und bestimmt dadurch das Steigungsdreieck (rot eingezeichnet).
eine direkte Propotionalität von x und y. Dabei
gibt m die Steigung des Graphs an und bestimmt dadurch das Steigungsdreieck (rot eingezeichnet).
Die lineare Funktion
Zeichnet man die Graphen der Funktionen f: f(x) = 0,5x , g: g(x) = 0,5x + 0,5 und h: h(x) = 0,5x - 0,5, so erkennt man, dass die Graphen zueinander parallel sind. Außerdem schneiden sie die y-Achse an dem Wert des zweiten Summanden (z.B. g: 0,5). Diesen Punkt nennt man y-Achsenabschnitt.
Eine Funktion f: f(x) = mx + t heißt lineare Funktion, die die Steigung m besitzt und deren Graph die y-Achse im Punkt P (0/t) schneidet.
Eigenschaften
- Die Nullstelle(n) N ist der Punkt, in dem der Graph die x-Achse schneidet.
- Den Schnittpunkt zweier Graphen kann man ausrechnen, indem man die beiden Gleichungen gleichsetzt, nach x auflöst und diesen Wert in eine der Gleichungen einsetzt.
- Stehen zwei Geraden aufeinander (f ⊥ g), so gilt der Zusammenhang
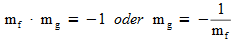
Ungleichungen
Eine Ungleichung entsteht, wenn zwei (oder mehr) Terme durch ein Ungleichheitszeichen miteinander verbunden sind. Bei folgenden äquivalenten Umformungen bleibt die Lösungsmenge gleich:
- Addition bzw. Subtratkion desselben Terms auf beiden Seiten
- Multiplikation bzw. Division desselben positiven Terms
- Multiplikation bzw. Division desselben negativen Terms bei gleichzeitiger Vertauschung des Ungleichheitszeichen
Lineare Gleichungssysteme: Rechnerisches Lösen
Zum Finden des Schnittpunkts von zwei Geraden gibt es verschiedene Möglichkeiten, die im Folgenden erklärt werden.
Das Gleichsetzungsverfahren
- Als erstes werden beide Gleichungen nach der gleichen Variable aufgelöst.
- Beide Terme werden gleichgesetzt.
- Die so enthaltene Lösung, die nur noch eine Unbekannte enthält, wird gelöst.
- Die Lösung wird in eine Gleichung eingesetzt und die andere Variable berechnet.
Beispiel
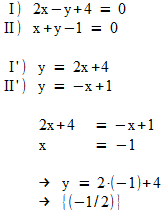
Das Einsetzverfahren
- Eine Gleichung wird nach einer Variable aufgelöst.
- Dieser Term wird in die andere eingesetzt.
- Die so erhaltene Lösung mit nur einer Variable wird gelöst.
- Die Lösung wird in eine Gleichung eingesetzt und die andere Variable berechnet.
Beispiel
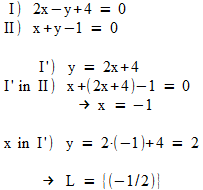
Das Additionsverfahren
Unterscheiden sich (nur) die Koeffizienten einer Variable in den Gleichungen, so empfiehlt sich das Additionsverfahren.
- Dazu werden zunächst die beiden Seiten der Gleichungen addiert. Dabei fällt eine Variable weg.
- Die erhaltene Gleichung mit einer Variable wird gelöst.
- Die andere Variable wird berechnet.
Fällt keine der beiden Unbekannten sofort durch bloßes Addieren (1.) weg, muss man eine (oder beide) Gleichung(en) vor dem Addieren mit einem geeigneten Faktor multiplizieren.
Beispiel
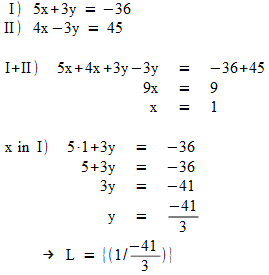
Laplace-Experimente
Das Zufallsexperiment
Unter dem Begriff Experiment versteht man Vorgänge, die man unter gleichen Bedingungen beliebig oft wiederholen kann. Dabei kann man zwischen zwei Arten unterscheiden:
- Deterministische Experimente (lat. determinare = bestimmen): Das Ergebnis kann in eindeutiger Weise vorhergesagt werden, wie z.B. die Fallgeschwindigkeit aus einer bestimmten Höhe.
- Zufallsexperimente: Das Ergebnis eines Versuchs ist nicht eindeutig vorhersehbar; der Zufall spielt eine Rolle; z.B. das Werfen einer Münze.
Die Menge aller möglichen Ergebnisse eines Zufallsexperiments fasst man zu einer Menge zusammen, der Ergebnismenge oder dem Ergebnisraum Ω. Die einzelnen Ergebnisse bezeichnet man als ω1, ω2 etc.
Das Ereignis
Eine Münze wird dreimal geworfen. Dabei können verschiedene Ereignisse eintreten:
- Die Beschreibung „beim ersten Wurf Kopf“ passt auf die Ereignisse KKK, KZK, KKZ, KZZ. Man sagt, das Ereignis A: „beim ersten Wurf Kopf“ ist eingetreten und schreibt A = {KKK, ..., KZZ}. Diese Ergebnisse nennt man günstige Ergebnisse.
- Die Ergebnisse ZZZ, ZKK, ZKZ, ZZK sind bei diesem Ereignis nicht eingetreten und man schreibt
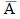 = {...} (gesprochen: A quer). Es ist das Gegenereignis.
= {...} (gesprochen: A quer). Es ist das Gegenereignis. - „Niemals Zahl“ enthält nur B = {KKK}. Dieses Ereignis nennt man Elementarereignis.
- Das Ereignis C: „Kopf oder Zahl“ tritt sicher auf; es wird deshalb als sicheres Ereignis bezeichnet: C = {...} = Ω.
- Das Ereignis D: „Gleichzeitig Kopf und Zahl“ heißt das unmögliche Ereignis.
Das Zählprinzip
Möchte man n Dinge anordnen, so gibt es ![]() Möglichkeiten. Außerdem gilt 0! = 1! = 1.
Möglichkeiten. Außerdem gilt 0! = 1! = 1.
Gebrochenrationale Funktionen
Einfache gebrochenrationale Funktionen sind z.B.
Beispiele für gebrochenrationale Funktionen
Eine gebrochenrationale Funktion ist ein Term, dessen Nenner die unabhängige Variable x enthält. Dadurch können im Nenner Nullstellen auftreten, was bewirkt, dass die Funktion an dieser stelle eine Definitionslücke bzw. eine Polstelle besitzt.
Um diesen x-Wert herauszufinden setzt man den Nennerterm gleich null; das Ergebnis der Gleichung ist die Definitionslücke:
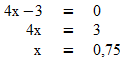
An dieser Stelle (x = 0,75) nähert sich der Graph von beiden Seiten dieser senkrechten Amplitude an, ohne sie zu berühren. Die waagrechte Amplitude erhält man, indem man den Zähler und Nenner durch x teilt und für x sehr große und sehr kleine Werte definiert:
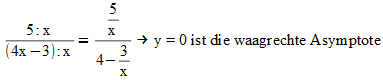
Strahlensätze und Ähnlichkeit
Ähnlichkeit
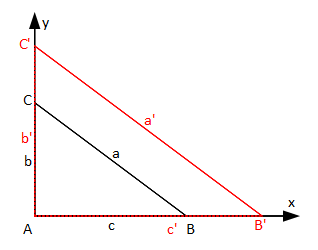
Gegeben sind die Dreiecke ABC mit A(0/0), B(4/0), C(0/3) und AB′C′ mit B′(6/0) und C′(0/4,5).
Vergleicht man Streckenlängen miteinander kann man folgendes erkennen:
a′ = 7,5 cm ; a = 5 cm
b′ = 4,5 cm ; b = 3 cm
c′ = 6,0 cm ; c = 4 cm
Der Quotient zweier Länge, der eien Zahl ist, heißt „Verhältnis der Längen“. Betrachtet man den/die Quotient(en), erhält man
Jede Strecke vom Dreieck AB′C′ ist um den Streckfaktor k = 1,5 gegenüber dem Dreieck ABC länger. Sie sind deshalb zueinander ähnlich.
Der Vierstreckensatz oder Strahlensatz
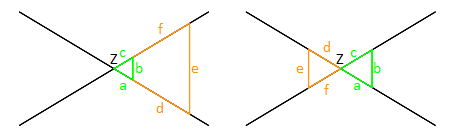
Werden zwei Geraden, die einander im Punkt Z scheiden, von zwei Parallelen geschnitten, so verhalten sie sich wie folgt:
- Je zwei Abschnitte auf der einen Geraden wie die entsprechenden Abschnitte auf der anderen.
- Die Abschnitte auf den Parallelen wie die von Z aus gemessenen entsprechenden Abschnitte auf der einen Geraden (bzw. der anderen)