- Astronomische Weltbilder
- Entwicklung des astronomischen Weltbilds
- Kopernikanische Wende
- Die Keplerischen Gesetze
- Erstes keplerisches Gesetz
- Zweites keplerisches Gesetz
- Drittes keplerisches Gesetz
- Aspekte der modernen Kosmologie
- Größe der Milchstraße
- Geburt des Weltalls
- Mechanik Newtons
- Newtons Gesetze
- Zusammensetzung von zwei wirkenden Kräften
- Wirken in eine Richtung
- Wirken in entgegengesetzte Richtungen
- Anderweitiges Wirken
- Newton I – Das Trägheitsgesetz
- Newton II – Das newtonsche Grundgesetz
- Newton III – Das Wechselwirkungsgesetz
- Eindimensionale Bewegungen
- Bewegungsdiagramme
- Gleichförmige geradlinige Bewegung (a = 0)
- Gleichmäßig beschleunigte geradlinige Bewegung (F = konst. ≠ 0)
- Beschleunigte geradlinige Bewegung (a ≠ konst.)
- Harmonische Schwingungen
- Fadenpendel
- Federpendel
- Energie als Erhaltungsgröße
- Impuls als Erhaltungsgröße
- Zweidimensionale Bewegungen
- Waagerechter Wurf
- Gleichförmige Kreisbewegung
- Zentripetalkraft
- Gravitationsgesetz
- Grenzen der Gültigkeit der newtonschen Mechanik
- Kausalitätsprinzip
- Spezielle Relativitätstheorie
- Längenkontraktion und Zeitdilation
- Addition von Geschwindigkeiten
- Relativität der Masse
- Äquivalenz von Masse und Energie
- Wellenlehre und Einblick in die Quantenphysik
- Wellenphänomene in verschiedenen Bereichen der Physik
- Entstehung und Arten von Wellen
- Beschreibung mechanischer Wellen
- Ausbreitung einer Welle
- Eigenschaften von Wellen
- Wellen- und Teilchencharakter des Lichts
- Licht und seine Eigenschaften
- Beugung von Licht
- Interferenz von Licht
- Frequenz und Wellenlängen von Licht
- Bedingungen für Verstärkung und Auslöschung
- Fotoeffekt
- Quantenobjekte – Elektronen, Photonen, Masseteilchen
- Quantenobjekte
- Teilchencharakter von Elektronen
- Wellencharakter von Elektronen
- Elektronen im Doppelspalt-Experiment
- Zufall in der Quantenphysik
- Literatur und Quellen
Astronomische Weltbilder
Entwicklung des astronomischen Weltbilds
Schriftlich fixiert wurden die ersten astronomischen Entdeckungen nicht, sondern wurden in Bauten und Darstellungen festgehalten, um so ein Zeitmaß zu erhalten. Dabei wurden vor allem Sonne und Mond genutzt.
Die Griechen nutzten babylonische und ägyptische Quellen, um ein Weltbild zu erschaffen. Daraus entstand das geozentrische Weltbild, in dem die Erde im Zentrum des Sonnensystems liegt und sich die anderen Planeten sowie die Sonne um jene auf Kreisbahnen bewegen.
Hipparch (190-125 v. Chr.) erstellte einen Sternenkatalog mit ca. 1000 Sternen. Darin waren die Orte und die Helligkeit der Sterne enthalten. Die Leistung der Griechen wurde von Claudius Ptolemäus in dem Buch „Syntaxis mathematicae“ (mathematische Zusammenhänge) bzw. der Almagest zusammengefasst.
Im geozentrischen Weltbild kam es aber zu Ungereimtheiten, z.B., dass sich ein Planet schleifenförmig bewegt; daraus wurde die Theorie entwickelt, dass sich der Planet auf dem Epizykel bewegt, der auf dem Deferent wandert. Dessen Mittelpunkt liegt nicht im Weltzentrum.
Es gab jedoch auch Griechen, wie Aristarch (310-230 v. Chr.), die das heliozentrische Weltbild vertraten, d.h. ein Sonnensystem, in der die Sonne im Zentrum liegt und sich die Planeten – also auch die Erde – um sie herum bewegen.
Kopernikanische Wende
Nikolaus Kopernikus (1473-1543) legte um 1510 Thesen dar und leitete so die kopernikanische Wende ein:
- Der Erdmittelpunkt ist der Mittelpunkt der Mondbahn.
- Die Himmelskörper bewegen sich um die Sonne.
- Die Fixsternsphäre ist unendlich weit entfernt.
- Die Bewegung des Fixsternhimmels ist Folge der Erdrotation.
- Die Erde rotiert sich um sich selbst und um die Sonne.
- Die Bewegung der Planeten ist Resultat der Planetenbewegung und der Erdenbewegung um die Sonne.
Die Keplerischen Gesetze
Erstes keplerisches Gesetz
Die Planeten bewegen sich auf elliptischen und nicht auf runden Bahnen um die Sonne. Sie steht im Brennpunkt einer solchen Ellipse.
Zweites keplerisches Gesetz
Die Bewegung eines Planeten ist konstant. Dabei gilt:
Der Planet legt also bei gleicher Zeit die gleiche Fläche zurück.
Drittes keplerisches Gesetz
Der Zusammenhang zwischen Umlaufzeiten und großen Halbachsen für zwei Planeten lautet:
Aspekte der modernen Kosmologie
Die Kosmologie ist ein Teilgebiet der Astronomie und umfasst die Lehre vom Ursprung und der Entwicklung des Universums. Die Erfahrungen und Entdeckungen kann man im kosmologischen Prinzip zusammenfassen: Kein Punkt im Weltall ist ausgezeichnet.
Große Entfernungen werden in Parsec (1 pc) angegeben. Ein Parsec beträgt 3,26 Lichtjahre:
Größe der Milchstraße
So hat die Milchstraße am Zentralgebiet senkrecht zur Scheibenebene eine Ausdehnung von 5000 pc. In diesem Zentralgebiet befindet sich vermutlich ein Schwarzes Loch.
Diese „Scheibe“ umschließen kugelförmige Sternenhaufen, die den galaktischen Halo bilden. Dieser hat einen Radius von circa 25 kpc (Scheibenebene: 30.000 pc). Dabei liegt die Milchstraße in einer Korona, einer Hülle aus dunkler Materie.
Geburt des Weltalls
Unser Universum verändert sich stetig. Die Galaxien entfernen sich nach dem hubbleschen Gesetz. Diese Geschwindigkeit nennt man Fluchtgeschwindigkeit v:
Die Fluchtgeschwindigkeit nimmt also mit zunehmender Entfernung r immer weiter zu. Diesen Zusammenhang hat man auch zur Bestimmung des Alters des Universums verwendet: Rechnet man zurück, kommt man so auf ein ungefähres Alter des Weltalls von 13,81 Milliarden Jahren.
Durch die Ausdehnung konnte sich auch Strahlung gleichmäßig verteilen, die als 3-K-Hintergrundstrahlung bezeichnet wird, da sie ungefähr 2,725 Kelvin beträgt.
Mechanik Newtons
Newtons Gesetze
Zusammensetzung von zwei wirkenden Kräften
Hat man zwei Kräfte, die auf einen Körper wirken, stellt man sich die Frage, wie dieser bewegt wird. Hierfür ist maßgeblich, wie sich die Kräfte zueinander verhalten.
Wirken in eine Richtung
Wirken die untersuchten Kräfte in eine Richtung, so kann man die Beträge addieren. Die Kräfte werden durch Pfeile dargestellt, deren Länge der jeweiligen Stärke entspricht. Man erhält durch das Aneinanderlegen dieser die Gesamtkraft.
Wirken in entgegengesetzte Richtungen
Wirken die Kräfte entgegengesetzt, zeigen die Pfeile also in die umgekehrte Richtung, so subtrahiert man sie.
Anderweitiges Wirken
Wirken die Kräfte anderweitig zueinander (sie wirken also nicht parallel), so erhält man die Gesamtkraft mithilfe eines Kräfteparallelogramms, in dem die beiden Kräfte je zwei Seiten darstellen.
Newton I – Das Trägheitsgesetz
Das erste newtonsche Gesetz setzt sich mit der Trägheit von Körpern auseinander. Demnach setzt ein Körper seinen momentanen Zustand fort, wenn auf ihn keine Kraft wirkt oder die auf die ihn einwirkenden Kräfte in der Summe 0 ergeben.
Newton II – Das newtonsche Grundgesetz
Nach dem newtonschen Grundgesetz gilt Folgendes: Wirkt auf einen Körper der Masse m eine Kraft F, so erfährt er die Beschleunigung a.
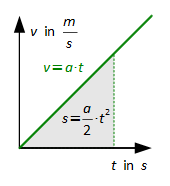
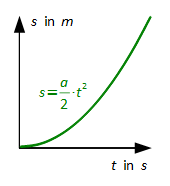
Für die gleichmäßige Beschleunigung eines Körpers aus dem Stillstand gelten, wenn die Beschleunigung a konstant ist, folgende Zusammenhänge:
Newton III – Das Wechselwirkungsgesetz
Nach dem Wechselwirkungsgesetz gilt: Wirken zwei Körper aufeinander, so wirkt auf beide Körper eine gleich große entgegengesetzt gerichtete Kraft:
Eindimensionale Bewegungen
Bewegungsdiagramme
Gleichförmige geradlinige Bewegung (a = 0)
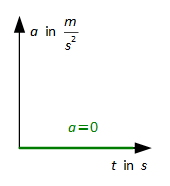
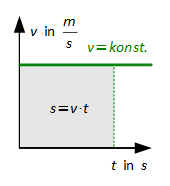
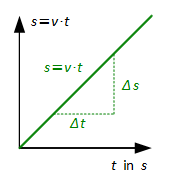
Gleichmäßig beschleunigte geradlinige Bewegung (F = konst. ≠ 0)
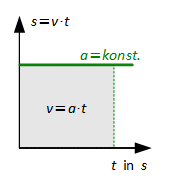
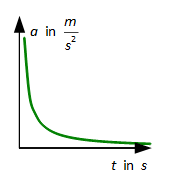
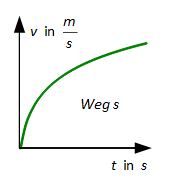
Beschleunigte geradlinige Bewegung (a ≠ konst.)
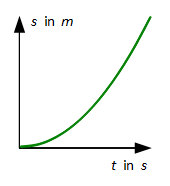
Harmonische Schwingungen
Eine mechanische Schwingung ist eine zeitlich periodische Bewegung eines Körpers um eine Gleichgewichtslage. Zum Erzeugen müssen folgende Dinge vorhanden sein:
- Schwingungsfähiger Körper
- Körper ausgelenkt aus seiner Gleichgewichtslage (Kraft bzw. Energie benötigt)
- Kraft, die den Körper zu Gleichgewichtslage zurücktreibt
Ein Beispiel ist etwa, wenn eine Masse m an ein Federpendel gehängt und aus der Gleichgewichtslage gelenkt wird.
Es wirkt eine Federkraft F:
Daraus ergibt sich wiederum folgende Gleichung:
Eine Schwingung, bei der die zurücktreibende Kraft F ∼ Auslenkung y ist, nennt man harmonische Schwingung. Als Auslenkung y bezeichnet man den Abstand zur Gleichgewichtslage, der Elongation. Hat man ein t-y-Diagramm mit einer harmonischen Schwingung, so ist deren Graph eine Sinuskurve. Jene werden deshalb auch Sinusschwingung genannt.
Die Amplitude A (Einheit: 1 m) ist der größte Abstand des schwingenden Körpers zur Ruhelage. Die Schwingungs- bzw. Periodendauer ([T] = 1 s) gibt die Zeit für eine Schwingung an. Die Frequenz f einer Schwingung gibt an, wie viele Schwingungen pro Sekunde ablaufen.
- Formelzeichen: f
- Einheit: 1 Hertz bzw. $\mathrm{1\,Hz = 1 \cdot s^{-1}}$
Die Frequenz kann berechnet werden mit:
Dabei ist T die Schwingungsdauer, n die Anzahl der Schwingungen und t die benötigte Zeit für n Schwingungen.
Für die harmonische Schwingung lautet die Funktionsgleichung y(t):
A ist hier die Amplitude, t die Zeit, T die Schwingungsdauer und ω die Kreisfrequenz.
Fadenpendel
Für die Schwingungsdauer eines Fadenpendels gilt unter Bedingung der kleinen Auslenkung aus der Ruhelage:
Dabei ist l die Länge des Fadenpendels.
Federpendel
Für die Schwingungsdauer eines Federpendels gilt:
Dabei ist m die Masse des schwingenden Körpers und D die Federkonstante
Energie als Erhaltungsgröße
Mit Energie kann ein Körper verformt, erwärmt oder zur Strahlenaussendung gebracht werden. In einem abgeschlossenen System bleibt die Gesamtenergie E erhalten, es gilt:
Impuls als Erhaltungsgröße
Der Impuls p ist das Produkt aus der Masse m und der Geschwindigkeit v:
In einem abgeschlossenen System bleibt der Gesamtimpuls P erhalten:
Zweidimensionale Bewegungen
Waagerechter Wurf
Ein waagerechter Wurf setzt sich aus einer gleichförmigen Bewegung in x-Richtung und einer in vertikaler Richtung gleichförmigen Bewegung zusammen, die unabhängig voneinander sind. Dabei gilt für den Aufenthaltsort eines Körpers nach einer bestimmten Zeit t:
Die Bahnkurve ist Teil einer Parabel:
Die Wurfdauer t ist nur von der Höhe h abhängig:
Die Wurfweite ist abhängig von der Anfangsgeschwindigkeit v0 und von der Höhe h:
Gleichförmige Kreisbewegung
Zu unterscheiden sind Kreis- und Drehbewegungen. Eine Kreisbewegung ist vorhanden, wenn der Körper als Massepunkt angesehen werden kann, z.b. bei einer Gondel eines Riesenrads. Die Drehbewegung ist z. B. die Bewegung des Riesenrads an sich. Ein Vergleich beider zeigt:
- Der Betrag der Geschwindigkeit ist konstant
- Bei der gleichförmigen Kreisbewegung ändert sich die Richtung der Geschwindigkeit; es liegt eine beschleunigte Bewegung vor
Die Geschwindigkeit v ist dabei abhängig vom Radius der Kreisbahn r und der Umlaufzeit T:
Die Winkelgeschwindigkeit ω gibt an, wie schnell sich der Drehwinkel φ (oder φ in Bogenmaß) ändert. Die Einheit ist deshalb der Quotient aus der Änderung des Winkels in einer bestimmten Zeit:
Bei einer gleichförmigen Kreisbewegung gilt für die Geschwindigkeit v:
Daraus ergibt sich, dass – unter der Bedingung, dass die Winkelgeschwindigkeit ω konstant ist – die Geschwindigkeit v größer wird, wenn der Radius r größer wird und dass bei konstantem Radius die Geschwindigkeit größer wird, je größer die Winkelgeschwindigkeit ist.
Zentripetalkraft
Die Zentripetalkraft FZ wird benötigt, um einen Körper auf einer gleichförmigen Kreisbahn zu bewegen. Die Kraft ist auf den Mittelpunkt des Kreises gerichtet. Für die Zentripetalkraft einer gleichförmigen Kreisbewegung gilt:
Bewegt sich der Körper auf der Kreisbahn, so wirkt eine gleich große entgegengesetzte Kraft, die Zentrifugalkraft.
Gravitationsgesetz
Zwischen einem Körper der Masse m und einem zweiten Körper der Masse M wirken Anziehungs- bzw. Gravitationskräfte. Die wirkende Gravitationskraft FG ist neben den Massen auch vom Abstand r der Massenmittelpunkte abhängig:
Dabei ist G die Gravitationskonstante:
Grenzen der Gültigkeit der newtonschen Mechanik
Kausalitätsprinzip
Für viele Bereiche der Physik, Technik und des Alltags gilt das Prinzip der starken Kausalität: Ähnliche Ursachen haben ähnliche Wirkungen.
Es gibt aber auch Situationen, in denen die Anfangsbedingungen leicht verändert werden können und die Wirkungen sehr variieren. Die starke Kausalität ist verletzt, obwohl die Aussage der gleichen Wirkung bei gleicher Ursache gelten kann. Man nennt dies das Prinzip der schwachen Kausalität.
Liegt eine starke Kausalität in einem System vor, dann auch eine schwache. Das Verhalten könnte man bei exakter Kenntnis der Bedingungen vorhersagen, was in der Praxis jedoch nicht möglich ist. Man spricht hier vom deterministischen Chaos. Die Verletzung der starken Kausalität führt zu Vorgängen, die auf lange Zeit hin betrachtet nicht vorhersagbar sind.
Spezielle Relativitätstheorie
Albert Einstein (1879-1955) begründete die spezielle Relativitätstheorie, die auf den Prinzipien der Relativität und der Konstanz der Lichtgeschwindigkeit beruht.
Das Relativitätsprinzip besagt, dass sich in mit konstanter Geschwindigkeit zueinander bewegenden Bezugssystemen die physikalischen Gesetze gleich wirken. Das zweite Prinzip besagt, dass sich Licht im Vakuum immer mit der Lichtgeschwindigkeit c ausbreitet:
Längenkontraktion und Zeitdilation
Betrachtet man Körper und Uhren, die sich relativ zu einem Beobachter schnell bewegen, scheinen die Körper sich für diesen in Bewegungsrichtung zu verkürzen bzw. gehen die Uhren langsamer. Wie groß die Effekte ausfallen, kann man mit dem Lorentzfaktor γ herausfinden:
Aufgrund dieser Formel ist es auch nicht möglich, die Lichtgeschwindigkeit zu erreichen oder zu übersteigen. Wäre die Geschwindigkeit v so groß wie die Lichtgeschwindigkeit, hätte man im Nenner des Bruchs 0, was nicht berechenbar ist.
Um die Längenkontraktion zu erhalten, muss man den Faktor γ mit der Länge des Körpers in Verbindung setzen:
Bei der Zeitdilatation gilt:
Addition von Geschwindigkeiten
Für Geschwindigkeiten unter zehn Prozent der Lichtgeschwindigkeit gilt, dass die Summe der Geschwindigkeiten v1 und v2 die Geschwindigkeit v ergibt:
Über dieser „Grenze“ ist dies nicht der Fall, da relativistische Effekte eine Rolle spielen. Die Geschwindigkeiten addieren sich so, dass die Summe immer kleiner oder gleich der Lichtgeschwindigkeit ist.
Relativität der Masse
Je näher die Geschwindigkeit v eines Körpers oder Teilchens der Lichtgeschwindigkeit c kommt, desto mehr nimmt seine Masse zu:
Äquivalenz von Masse und Energie
Die Gesamtenergie E eines Körpers ist proportional zu seiner Masse m. Es gilt:
Da c eine Konstante ist, sind Energie und Masse das Gleiche mit unterschiedlichen Einheiten. Dabei entspricht eine Energie von 1 J einer Masse von circa 10-14 g.
Wellenlehre und Einblick in die Quantenphysik
Wellenphänomene in verschiedenen Bereichen der Physik
Man kann zwischen mechanischen Wellen, die mechanische Größen verändern, und elektromagnetischen Wellen, die die Stärke elektrischer und magnetischer Felder verändern, unterscheiden.
Entstehung und Arten von Wellen
Voraussetzungen für mechanische Wellen sind:
- Schwingungsfähige Körper bzw. Teilchen
- Körper müssen untereinander „kräftemäßig“ gekoppelt sein
- Einzelne Körper müssen aus der Gleichgewichtslage ausgelenkt sein
Durch Kopplungen können Körper die Energie naher Schwinger aufnehmen, wodurch die Ausbreitung über mehrere Medien ablaufen kann. Alle Schwinger bilden die mechanische Welle.
Man unterscheidet Longitudinal- und Transversalwellen. Bei den Longitudinalwellen (Längswellen) sind die Ausbreitungsrichtung und die Schwingungsrichtung gleich. Bei den Transversalwellen (Querwellen) ist die Schwingung senkrecht zur Ausbreitung. Wellen können Energie, aber keine Stoffe transportieren.
Beschreibung mechanischer Wellen
Zur Beschreibung einer Welle können Schwingungsgrößen wie Elongation, Amplitude, Schwingungsdauer und Frequenz genutzt werden. Die Ausbreitung einer Auslenkung wird mit der Wellenlänge λ (in Metern) und der Wellengeschwindigkeit beschrieben. Die Wellenlänge ist der Abstand eines Schwingers zum nächsten im gleichen Schwingungszustand.
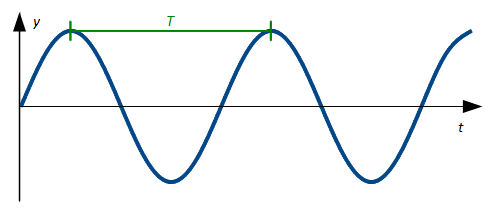
Für einen bestimmten Ort (x = konstant) wird im nebenstehenden t-y-Diagramm dargestellt, wie sich der einzelne Schwinger in Abhängigkeit von der Zeit bewegt.

Für einen bestimmten Zeitpunkt (t = konstant) wird dargestellt, welche Elongationen die verschiedenen Schwinger besitzen.
Ausbreitung einer Welle
Die Ausbreitungsgeschwindigkeit v ist die Geschwindigkeit, mit der sich eine Welle ausbreitet.
Ein Wellenberg und -tal kann als Auslenkung angesehen werden. Die Geschwindigkeit ist umso stärker, je größer die Kupplungskräfte zwischen den Teilchen eines Stoffes sind und (in der Regel) je höher die Temperatur ist. Dabei gilt:
Es ist zu beachten, dass die Frequenz einer Welle abhängig vom Medium ist und sie sich bei der Ausbreitung nicht ändert, auch bei einem Übergang in einen anderen Stoff nicht. Dagegen ist aber die Geschwindigkeit vom Medium abhängig.
Eigenschaften von Wellen
Wellen breiten sich geradlinig aus und bilden eine Wellenfront. Das nach Christian Huygens benannte huygenssche Prinzip besagt, dass jeder Punkt einer Wellenfront Ausgangspunkt kreis- oder kugelförmiger Elementarwellen ist, die so schnell wie die ursprüngliche Welle sind. Durch die Überlagerung bilden sie eine neue Wellenfront.
Mechanische Wellen können reflektiert, gebrochen und gebeugt werden, d.h. sie breiten sich hinter einem Hindernis weiter aus. Überlagern sich Wellen mehrerer Erreger, so bilden sich Bereiche der Ruhe und stärkerer Schwingung, da sich die Elongationen addieren.
Nach der Überlagerung laufen sie unverändert weiter. Man nennt diese ungestörte Wellenüberlagerung gleicher Geschwindigkeit und gleicher Schwingungsrichtung Interferenz. Es treten Bereiche der Verstärkung und Abschwächung oder Auslöschung auf. Treffen zwei Wellenberge oder -täler aufeinander, ergibt sich eine maximale Verstärkung. Zu einer Auslöschung kommt es, wenn ein Wellenberg und einer Wellental gleicher Amplitude aufeinandertreffen.
Wellen- und Teilchencharakter des Lichts
Licht und seine Eigenschaften
Bisher ist aus den vorigen Themen bekannt, dass
- sich Licht geradlinig ausbreitet,
- Licht eine Geschwindigkeit von ca. 300.000 km/s hat,
- Licht beim Auftreffen auf ein Körper teilweise reflektiert wird,
- weißes Licht aus mehreren Farben besteht,
- Licht beim Auftreffen auf eine Grenzfläche optisch verschiedener Stoffe gebrochen wird,
- es beim Abgeben von Energie entsteht (die Lichtquanten oder Photonen) und
- Photonen im sichtbaren Bereich eine Energie von 1,5 eV bis 3,3 eV haben.
Beugung von Licht
Trifft Licht auf einen sehr schmalen Spalt, ein Hindernis oder eine Kante, so breitet es sich dahinter in verschiedene Richtungen aus. Dies wird Beugung genannt. Da dieses Phänomen wellentypisch ist, kann man annehmen, dass Licht Welleneigenschaften hat.
Interferenz von Licht
Wirft man Licht auf schmale Doppelspalte, kann man auf einem Schirm dunkle und helle Streifen erkennen, die auf eine Überlagerung hinweisen. Deutlicher wird der Effekt, wenn man ein Gitter verwendet. Ein Gitter besteht aus Spalten, deren Abstand man als Gitterkonstante bezeichnet.
Dies kann durch die Ansicht erklärt werden, dass sich Licht als Welle ausbreitet und sich an einem Hindernis Elementarwellen bilden, die sich überlagern. Licht hat somit Eigenschaften einer Welle und kann mit dem Modell der Lichtwelle beschrieben werden.
Frequenz und Wellenlängen von Licht
Im Wellenmodell lässt sich jeder Farbe eine bestimmte Frequenz und eine Wellenlänge zuordnen. Vom Charakter her ist Licht Teil der elektromagnetischen Wellen, da es eine elektromagnetische Welle darstellt.
Bedingungen für Verstärkung und Auslöschung
Im Folgenden wird betrachtet, was passiert, wenn Licht einer bestimmten Wellenlänge auf einen Doppelspalt trifft.
Bei beiden Spalten gehen Lichtwellen aus. Zu einem beliebigen Punkt müssen die Wellen einen bestimmten Weg zurücklegen. Deren Differenz nennt man Gangunterschied Δs. Von diesem hängt der Schwingungszustand ab.
Die maximale Verstärkung tritt auf, wenn der Gangunterschied 0, λ, 2, λ, ... beträgt, d.h. zwei Wellenberge oder -täler fallen zusammen. Es gilt:
Die maximale Abschwächung, also die Auslöschung, tritt auf, wenn Wellenberg und -tal aufeinandertreffen. Der Gangunterschied beträgt dann
Fotoeffekt
Als 1888 der Fotoeffekt entdeckt wurde, war er einer der ersten Effekte, der die Anwendbarkeit des Wellenmodells beim Licht infrage stellte. Man beobachtete ihn, als eine geschmirgelte, negativ geladene Zinkplatte mit unterschiedlichem Licht bestrahlt wurde. Man fand heraus, dass die Platte unter bestimmten Bedingungen entladen wird. Dies kam durch die Herauslösung von Elektronen aus der Platte zustande.
Als äußerer Fotoeffekt wird die Erscheinung vom Herauslösen von Elektronen aus einer Oberfläche durch Licht genannt. Untersuchungen mit weiteren Stoffen und verschiedenen Lichtintensitäten sowie -wellenlängen ergaben Folgendes:
- Zum Herausschlagen eines Elektrons ist eine bestimmte, vom Stoff abhängige Energie erforderlich; dies nennt man Ablöseenergie oder Austrittsarbeit.
- Die Energie des Lichts ist von der Wellenlänge abhängig. Je größer die Frequenz ist, desto größer ist die Energie des Photons.
- Der Fotoeffekt tritt auf, wenn die Photonenenergie größer oder gleich der Energie zur Elektronenherauslösung ist. Ist sie größer, so hat das Elektron zudem eine bestimmte kinetische Energie.
Das Wellenmodell ist nicht anwendbar, da eine Erhöhung der Intensität des Lichts keinen Fotoeffekt hervorruft. Das Photonenmodell hilft; es kann als Teilchenmodell angesehen werden.
Quantenobjekte – Elektronen, Photonen, Masseteilchen
Quantenobjekte
Die Dinge, mit denen sich die Quantenphysik beschäftigt, nennt man Quantenobjekte. Dazu gehören Elektronen, Photonen, Neutronen, Atome und Moleküle. Bei diesen Objekten können Erscheinungen auftreten, die mit der klassischen Physik nicht erklärbar oder vereinbar sind.
Teilchencharakter von Elektronen
Elektronen sind Teilchen mit einer Masse von
Sie besitzen eine negative Elementarladung e von
Elektronen bewegen sich in Stromkreisen, werden in Magnetfeldern abgelenkt und elektrische Felder beschleunigen oder lenken sie ab. Ihre kinetische Geschwindigkeit und die kinetische Energie sind bestimmbar. Da sie sich wie klassische Teilchen verhalten, besitzen Elektronen Teilchencharakter.
Wellencharakter von Elektronen
Beschleunigt man Elektronen zwischen einer Kathode und einer ringförmigen Anode und schickt sie dann durch eine dünne Folie, so erhält man keinen hellen Fleck, sondern ein charakteristisches Muster, das durch bewegte Elektronen erzeugt wird. Dafür sprechen, dass
- die das Muster bildenden Kreise enger werden, wenn man die Beschleunigungsspannung erhöht und
- sich die Ringstruktur verzerrt, wenn man einen Magneten in die Nähe des Schirms bringt.
Das Muster wird also durch Elektronen und durch Photonen erzeugt. Daraus kann man folgern, dass Elektronen sowohl Teilchen- als auch Welleneigenschaften aufweisen.
Elektronen im Doppelspalt-Experiment
Wenn Elektronen eine Wellenlänge zugeordnet werden kann, müssten sich, wie beim Licht, beim Schicken auf einen Doppelspalt Inferenzstreifen bilden. Man erwartet Häufungen auf zwei Streifen.
Das Ergebnis aber ist, dass bei wenigen Elektronen ein zufälliges Muster, bei mehreren Elektronen ein Inferenzmuster wie beim Licht entsteht. Für einzelne Elektronen lässt sich das Ergebnis nicht vorhersagen, bei einer großen Anzahl schon.
Zufall in der Quantenphysik
Das Ergebnis eines Experiments mit Elektronen und Photonen hängt stark mit der Anzahl der Teilchen zusammen. Wenn man zum Beispiel schräg auf Glas Licht wirft, so wird ein Teil reflektiert und der Rest durchgelassen. Es wird angenommen, dass 75% des Lichts durchgelassen wird.
Werden einzelne Photonen geschickt, können sie entweder reflektiert oder durchgelassen werden. Was passiert, ist aber nicht vorhersehbar. Bei einer kleinen Anzahl ist das Verhältnis nicht wie oben beschrieben. Erst bei einer größeren Anzahl wird dieses Ergebnis ungefähr erreicht. Dieses Zufallsverhalten nennt man stochastisch.
Quantenobjekten ist kein Modell komplett zuordbar, da sie Welliges (Bestimmung der Ausbreitungen), Körniges (Teilchenhaftes, bei der Ortsbestimmung) und Stochastisches (Aussagen über Wahrscheinlichkeiten) aufweisen.
Sie unterscheiden sich deshalb von den makroskopischen Körpern, da bei diesen die Eigenschaften der Quantenobjekte nicht wichtig sind.
Literatur und Quellen
- Deger, Hermann: Galileo 10, 1. Auflage 2008, Oldenbourg Verlag, ISBN 978-3-637-00096-4
- Donat, Martin: Impulse Physik 10, 1. Auflage 2008, Klett Verlag, ISBN 978-3-127-72465-3
- Fösel, Angela/Gattermann, Thomas: Fokus Physik 10, 1. Auflage 2008, Cornelsen Verlag, ISBN 978-3-464-85318-4
- Meyer, Lothar/Gau, Barbara: Physik 10, 1. Auflage 2008, Duden Paetec, ISBN 978-3-835-53061-4